The Gambler’s Fallacy And The Law Of Large Numbers

The Gambler’s Fallacy (which is also known as the Monte Carlo Fallacy or the Fallacy Of The Maturity Of Chances) is one of a long list of fallacies, and one that is probably responsible for the loss of huge amounts of money over the centuries, not to mention the ruination of many people – all because they do not understand the nature of probability.

And that’s not surprising really – probability starts off as a relatively simple concept, but quickly becomes increasingly complex.

(If you were wondering, it’s called the Monte Carlo Fallacy because on August 18, 1913, at the casino in Monte Carlo, black came up on the roulette table a record twenty-six times in succession.)

What Is The Gambler’s Fallacy?

But first, let’s define what the Gambler’s Fallacy is.

According to Dek Terrell’s article in the May 1994 issue of the Journal of Risk and Uncertainty, the gambler’s fallacy is “the belief that the probability of an event is decreased when the event has occurred recently.“

Here’s an example of what that means: if a coin is tossed ten times and on each of those ten tosses, heads show, then many (or maybe most) people will guess that tails is more likely to come on the next toss.

Here’s the thing though – coin tosses are 100% independent of what happened previously.

Every single time you toss a regular coin, the chances of heads or tails showing are equal. (Yes, there is a minute chance that the coin will land on its edge, but this is so rare that it is negligible when looking at the probabilities.)

Of course, there are a number of factors that can affect each coin toss, such as how much pressure is applied when tossing it, air currents, how the coin is held and positioned, and probably more, but overall, you can expect heads or tails with equal probabilities.

Without getting too technical here, when you toss a coin, there are two possible outcomes – heads and tails.

So the probability of one specific outcome is that outcome divided by the total possible number of outcomes.

In this case, a head will occur one out of two times, which is a 50% chance.

So, why is this so confusing for so many people?

It stems in part from the fact that we humans (and, probably, most animals) are wired to detect patterns.

For wild animals today, and for humans in their distant past, the ability to recognize patterns is vital for survival.

This is less the case for humans these days, of course, but our brains still look for patterns, so much so that they often find them when they aren’t even there.

And there’s actually a term for that experience of seeing faces, for example, that aren’t really present – pareidolia.

The Law Of Large Numbers

Another key factor in the Gambler’s Fallacy is a misunderstanding of the Law of Large Numbers, which is “a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and will tend to become closer to the expected value as more trials are performed.“

What this means is that, in the case of tossing a coin, while you would expect an equal number of heads and tails to show after an even number of tosses, this rarely happens in practice – you may find the actual number of heads vs. tails is radically different, even though the ratio between the two outcomes becomes ever more equal.

Years ago, when I was first reading about probability, I wrote computer programs to simulate coin tosses, and I can verify that the more tosses you make, the closer you get to a 50:50 split between the two outcomes.

Today, I have created an Excel spreadsheet instead that simulates 100,000 coin tosses, which you can download here. (Note that this spreadsheet file is 11.5 MB and that you’ll find descriptions of what each column means in comments that you can see if you hover over each column heading.)

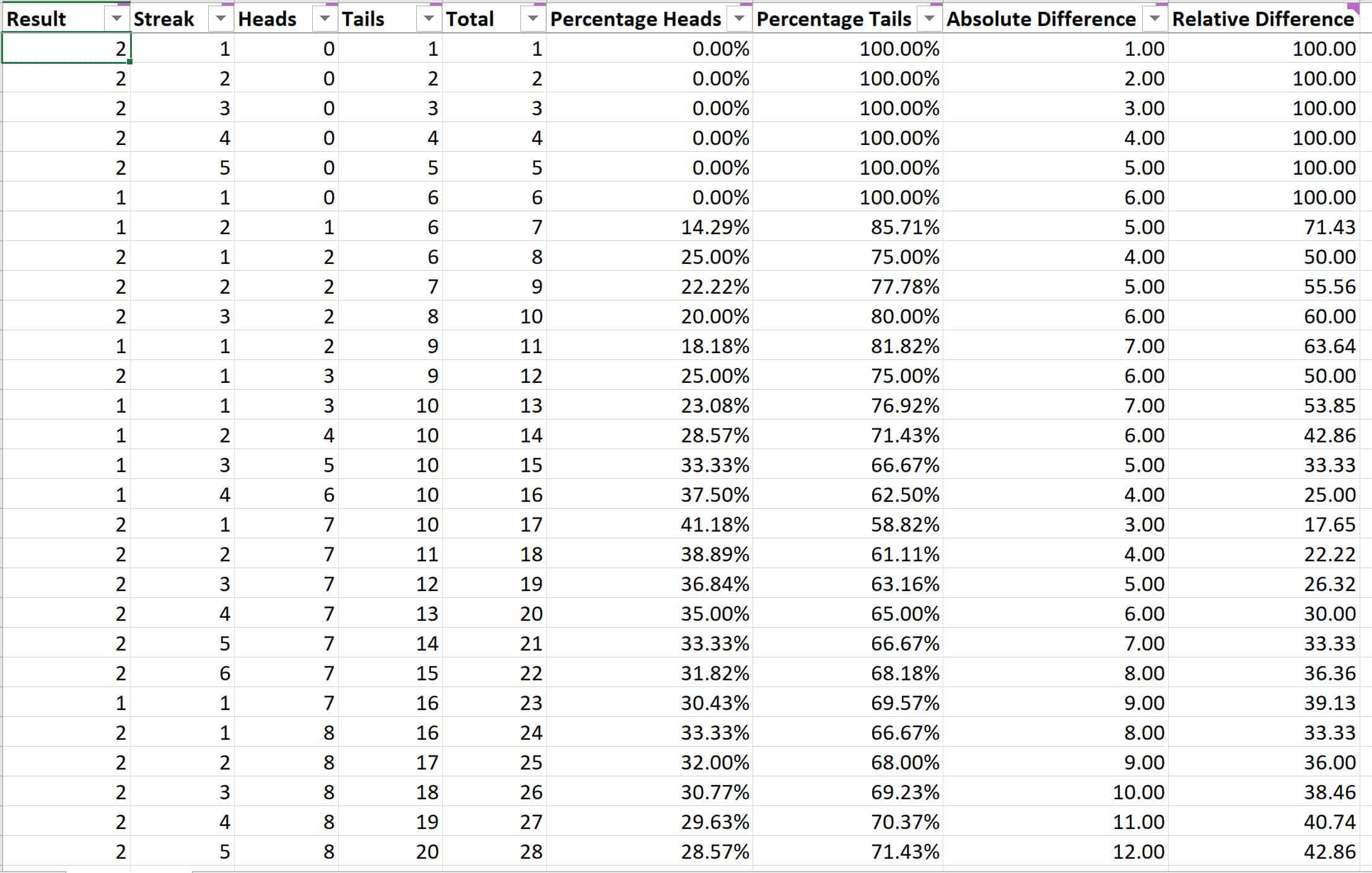
For those who cannot open it, here is a screenshot of the first 28 rows:

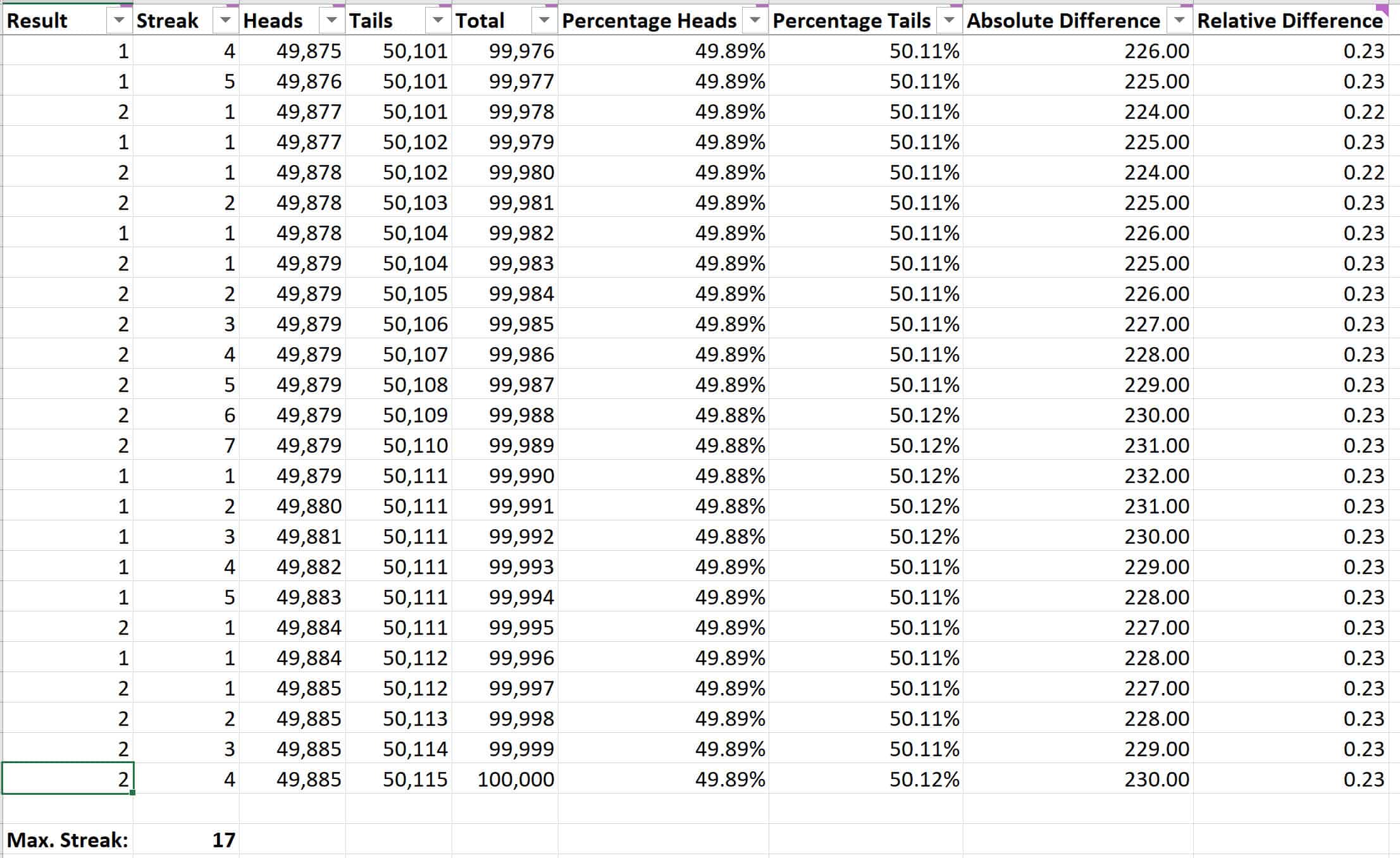
…and here is another screenshot of the last 25 rows:

As you can see from this spreadsheet (assuming you can open it – I’ve no idea whether this will open in other spreadsheet software, including Google Sheets) or the two screenshots:

1. The difference between the number of heads and number of tails usually varies and grows over time.
2. The ratio between the number of heads and tails starts off by varying erratically, but then it stabilizes so that the relative difference remains very close to 50:50.
3. The maximum streak can be much larger than you might at first guess. I refreshed the numbers (which you can do on a Windows PC by using the F9 key or selecting Formulas -> Calculate Now) several times, and the longest streak I have seen so far was 20.

Where the problem comes, for those who fall foul of the Gambler’s Fallacy, is that they think this law applies to small numbers too – and it doesn’t.

As you can see from the spreadsheet, when the number of coin tosses is low, you might see results that are a long way from 50:50, but when you increase the number of tosses, the ratio equalizes – and in the grand scheme of this type of simulation, 100,000 tosses is small, but I didn’t want to push my computer or spreadsheet software too hard.

But if you continued this experiment to, say, 1,000,000 tosses, you’d more than likely find the ratio is even closer to 50:50, even though the absolute difference between the number of heads and tails might be in the thousands.

So, back to our Gambler’s Fallacy.

After a longer-than-expected sequence of heads (e.g. ten), you’ll often hear people say something like, “Well, the Law of Averages says that a tail is due next”.

And here are the problems with that:

1. They are applying the Law of Large Numbers to too small a sample space.
2. Coin tosses are independent, which means that what happened on any previous tosses does not in any way affect the current toss. If this were the case, it would mean coins had some form of memory and a way to change whether heads or tails showed so as to “balance” things up, which is clearly not what happens.
3. These “laws” do not state that the outcome must absolutely be 50:50. They are more like observations of what tends to happen, given enough occurrences.

Examples Of The Gambler’s Fallacy In Action

While many of these fallacies can indeed be found within the world of gambling, they do exist elsewhere, so here are a few examples to show you what I mean:

• When starting a game where a coin toss is used to decide who plays first (or has the ball first, or whatever), if a team has lost their last three coin tosses, somebody might say that it’s their turn to win the toss – because of the “Law of Averages”.
• When Red comes up on the roulette table several times in a row, somebody will claim it must be time for Black to come up. (The origin of the Monte Carlo fallacy, as described above, shows this need not be the case.)
• Some people believe that, once a winning number has been drawn in the lottery, it won’t come up next time – because it’s not its turn until other numbers have been drawn.
• I used to choose six consecutive numbers back when I played the lottery in England, and people told me that such a sequence was highly unlikely to happen. They were correct in one way, but only because any set of six numbers was equally unlikely to be drawn. The lottery machine and balls do not have any memory of previous numbers drawn, and even if they did, there is no mechanism they could use to affect the next number drawn.
• If you read about the infamous “53 fever” (if that link doesn’t work, try this one) that occurred in Italy in the early 2000s, you’ll see that people went bankrupt and even died because of the Gambler’s Fallacy.
• When a family has three children of the same gender in a row, there is an expectation (and an unfounded one at that) that the next child will be the other gender.
• If somebody has had five good hands at cards in a row, some people will jump to the conclusion that the person’s next hand will not be good.
• Just because you have gone on ten job interviews in a row with rejections at each one, that does not mean you’ll be any more likely to get the next job you apply for.

In fact, many gambling “systems” rely on the Gambler’s Fallacy by having bettors look for a certain pattern (in a game or sport that is, essentially, random), and then bet based on that pattern.

And it’s one reason why most casinos make so much money – people will place bets based on this fallacy (e.g. it’s time for a black number to be selected) because they do not understand how probability works in the slightest. (The other reason casinos earn, not win, your money is, of course, because the odds are stacked in their favour.)

Conclusion

It’s relatively easy to get sucked into some form of Gambler’s Fallacy, and the main ways to defend against it are critical thinking skills and a basic understanding of probability.

Additional Resources

These are suggestions for those who wish to delve deeper into any of the above:

1. Critical Thinking
2. Innumeracy
3. Introductory Probability Course